Binary Alloys Chemistry Tutorial
Key Concepts
- Atoms in a pure metal solid are arranged in a regular crystal lattice.
- An alloy is a mixture of a metal with one or more other elements.
- A binary alloy is made up of two elements.1
- A homogeneous2 binary alloy is a solid solution:
The primary element is a metal and is called the solvent3.
The secondary element is called the solute.
- A homogeneous binary alloy can be classified as either substitutional or interstitial:
| Type of Alloy |
Relative Size of Atoms |
Description |
Example |
|---|
| Substitutional |
solute ≈ solvent |
Solute atoms substitute for solvent atoms in lattice. |
carbon steel |
|---|
| Interstitial |
solute < solvent |
Solute atoms occupy "holes" (interstices) in the solvent metal lattice. |
bronze, brass |
|---|
- An alloy exhibits metallic properties.
- Interstital and substitutional alloys are harder than the pure metal solvent.
Theory
In a sample of solid pure metal, the metal atoms are arranged in a regular 3-dimensional crystal lattice4.
We can picture a single layer of this metallic lattice as shown below:
 |
Each black circle is a 2-dimensional representation of a sphere.
Each sphere represents an atom of the same metallic element. |
These atoms are able to "roll over" each other making a pure metal malleable, ductile, and quite soft.
Metals such as pure iron, copper, tin, zinc, gold and lead are all quite soft.
Alloying, mixing, these metals with another element is a way of making them harder and therefore more useful.
Notice that there are spaces, or holes, between the metal atoms in the lattice:
 |
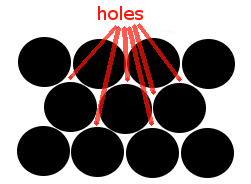These spaces, or holes, in the lattice are called interstices. |
One way for this metal to form a solid solution, a homogeneous alloy, is for atoms of another element to occupy some of these holes (interstices):
 |
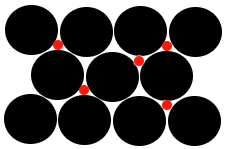The black circles represent the original metal atoms making up the lattice.
The red circles represent atoms of a different element inserted in the interstices.
Note that the atoms occupying the interstices must be much smaller than the metal atoms making up the original lattice. |
This type of alloy is known as an "Interstitial Alloy" because smaller atoms fit into the "holes" (interstices) in the existing metallic lattice.
Interstitial elements are often non-metals such as hydrogen, boron, carbon, nitrogen, oxygen and silicon.
The effect of having these small atoms occupy the interstices is that the large metal atoms are no longer able to roll over each other so easily when a stress is applied, that is, the alloy will be more rigid, less malleable and less ductile than the original pure metal.
There is another way in which a metal can form a homogeneous solid solution with another element, the metal atoms in the lattice can be replaced, or substituted, with atoms of a different element:
 |
The black circles represent the original metal atoms making up the lattice.
The red circles represent atoms of a different element which have substituted for some of the original metal atoms.
Note that these substituted atoms are a similar size to the metal atoms making up the original lattice. |
This type of alloy is known as a "Substitutional Alloy", that is, there has been a substitution of atoms in the metallic lattice for atoms of the other element that are of a similar size.
Typically, the atomic radii of the two types of atoms need to be within about 15% of each other so that they do not affect the overall crystal structure, which means that the solute atoms are most likely to metals.
The slightly different size of these solute atoms introduces strain in the lattice which strengthens the lattice making the resulting solid alloy more rigid, less malleable, less ductile, but of similar density to the original pure metal lattice.
Carbon Steel: Interstital Alloy
Pure iron is too soft to be useful. One way to make iron harder is to add a small amount by mass of carbon. The resulting alloy is known as carbon steel.
Carbon atoms are smaller than iron atoms as shown in the table below:
| atom |
radius5 / Å |
radius / m |
radius ratio |
|
volume6 / m3 |
volume ratio |
|---|
| carbon |
0.75 |
7.5 × 10-11 |
0.60 |
|
1.8 × 10-30 |
0.2 |
| iron |
1.24 |
1.24 × 10-10 |
1 |
|
8.0 × 10-30 |
1 |
The radius of a carbon atom is only 60% that of an iron atom, that is, the radius of a carbon atom is just a bit more than half the radius of an iron atom.
This means that the volume of space occupied by a carbon atom is only 20% of the volume of space occupied by an atom of iron.
Since an atom of carbon is much smaller than an atom of iron, carbon atoms can occupy the "holes", the interstices, in the lattice of iron atoms.
The carbon atoms are referred to as interstitial atoms, in this case, interstitial carbon atoms, and are shown as red circles in the diagram on the right with the iron atoms shown as the larger black circles.
In the carbon steel solid solution, iron is the solvent and carbon is the solute.
Carbon steel is made by adding about 1% by mass of carbon to iron.
In other words, every 100 g of carbon steel contains 1 g of carbon and 99 g of iron.
| Composition of 100 g of carbon steel |
|---|
| element |
% |
mass (g) = % × mass of steel (g) |
|---|
| carbon |
1% |
1% × 100 = 1/100 × 100 = 1 g |
|---|
| iron |
99% |
99% × 100 = 99/100 × 100 = 99 g |
|---|
Since we know the mass of carbon and iron making up a sample of carbon steel, we can calculate the ratio of carbon to iron atoms present in the lattice.
Let's assume we have a 100 g sample of carbon steel:
|
m
/g |
Mr
/ g mol-1 |
n / mol
n = m ÷ Mr |
N / atoms
N = n × NA |
ratio of atoms |
|---|
| carbon |
1.00 |
12.01 |
1.00 ÷ 12.08 = 0.0833 |
0.0833 × 6.02 × 1023
= 5.01 × 1022 |
(5.01 × 1022) ÷ (5.01 × 1022)
= 1 |
|---|
| iron |
99.00 |
55.85 |
99.00 ÷ 55.85 = 1.773 |
1.773 × 6.02 × 1023
= 1.067 × 1024 |
(1.067 × 1024) ÷ (5.01 × 1022)
= 21.30 |
|---|
The ratio of carbon atoms to iron atoms is about 1: 21.
That is, there is 1 atom of carbon for every 21 atoms of iron in the lattice.
The interstitial carbon atoms make the metal lattice more rigid, decreasing malleability and ductility.
Carbon steel is much harder than iron.
Bronze: Substitutional Alloy
The Copper Age (3200-2300 B.C.) is so called because of the proliferation of human artefacts made out of copper.
But copper is a soft metal so it is easily dented and corrodes readily. One way to make copper harder and more resistant to corrosion is to add tin, and this alloy is known as bronze.
Bronze was first produced by humans about 5,000 years ago making it the first manmade alloy and giving the Bronze Age (3200-1000 B.C.) its name.
The table below compares the size of tin atoms and copper atoms:
| atom |
radius / Å |
radius / m |
radius ratio |
|
volume / m3 |
volume ratio |
|---|
| tin |
1.4 |
1.40 × 10-10 |
1.15 |
|
1.15 × 10-29 |
1.5 |
| copper |
1.22 |
1.22 × 10-10 |
1 |
|
7.6 × 10-30 |
1 |
From the table we can see that the radius of an atom of tin is 1.15 times the radius of an atom of copper, that is, the radius of an atom of tin is only slightly larger than the radius of an atom of copper.
This means that the volume of space occupied by an atom of tin is also slightly more (1.5 times) more than the volume of space occupied by an atom of copper
Because atoms of tin and copper are of a similar size, tin atoms can substitute for some of the copper atoms in the metal lattice.
In the diagram on the right, copper atoms are represented by the black circles while the red circles represent atoms of tin which have substituted for some of the copper atoms.
In the bronze solid solution, copper is the solvent and tin is the solute.
Bronze is an alloy made up of 70-90% copper and 30-10% tin.
The composition of gun metal bronze is given below:
| Element |
% by mass |
mass element = % × mass of bronze
For 100 g sample of bronze: |
|---|
| tin |
10 % |
10/100 × 100 = 10 g |
|---|
| copper |
90% |
90/100 × 100 = 90 g |
|---|
We can use this data to calculate the ratio of tin to copper atoms in gun metal bronze:
|
m
/g |
Mr
/ g mol-1 |
n / mol
n = m ÷ Mr |
N / atoms
N = n × NA |
ratio of atoms |
|---|
| tin |
10.00 |
118.7 |
10.00 ÷ 118.7 = 0.08425 |
0.08425 × 6.02 × 1023
= 5.072 × 1022 |
(5.072 × 1022) ÷ (5.072 × 1022)
= 1 |
|---|
| copper |
90.00 |
63.55 |
90.00 ÷ 63.55 = 1.416 |
1.416 × 6.02 × 1023
= 8.526 × 1023 |
(8.526 × 1023) ÷ (5.072 × 1022)
= 16.81 |
|---|
The ratio of tin to copper atoms is approximately 1:17
Compared to the original pure copper lattice, only 1 in every 18 copper atoms has been substituted with a tin atom.
We can estimate the impact of this on the density of the alloy.
Consider 100 g of gun metal bronze. 10 g of this will be tin, 90 g will be copper. The density of pure tin and pure is known:
| element |
density / g cm-3 |
|---|
| tin |
7.31 |
|---|
| copper |
8.96 |
|---|
Since density = mass (g) ÷ volume (cm3) we can rearrange this equation to find the volume (cm3):
| density |
= |
mass
volume |
multiply both sides of the
equation by volume |
| density × volume |
= |
mass × volume
volume |
| which gives |
| density × volume |
= |
mass |
divide both sides of the
equation by density |
density × volume
density |
= |
mass
density |
| so |
| volume |
= |
mass
density |
Now we can calculate the volume of space occupied by 10 g of tin and 90 g of copper in the bronze alloy7:
| element |
density / g cm-3 |
mass / g |
volume / cm3
(= mass/density) |
|---|
| tin |
7.31 |
10 |
10 ÷ 7.31 = 1.4 |
|---|
| copper |
8.96 |
90 |
90 ÷ 8.96 = 10 |
|---|
The density of the alloy can then be calculated:
| density of alloy = |
mass of alloy
volume of alloy |
| density of alloy = |
mass of copper + mass of tin
volume of copper + volume of tin |
| density of alloy = |
10 + 90
1.4 + 10 |
| density of alloy = |
100
11.4 |
| density of alloy = |
8.8 g cm-3 |
We can see that the density of gun metal bronze is only slightly less than the density of pure copper.
We find there are other physical properties of the alloy, such as the melting point, which lie somewhere between the same property for each of the pure metals:
| Substance |
melting point / °C |
|---|
| tin |
232 |
| copper |
1803 |
| bronze |
950 |
By substituting some of the copper atoms for tin in the lattice, we make an alloy, bronze, which is harder than copper and has a lower density and melting point than copper which makes it easier to cast.
Since tin and copper are both metals, metallic bonds hold the lattice together so the alloy continues to exhibit the typical metallic properties of being ductile and malleable.
Bronze usually oxidises only superficially, that is, copper atoms oxidise to copper oxide which form a protective layer over the surface preventing further oxidation.
For this reason, and because bronze is easy to cast, it has been used to make statues, coins, bells and cymbals.
Bronze is also quite resistant to corrosion by seawater, so it is still used to make ship propellers.
Bronze is also used for bearings because it has very low metal-on-metal friction, placing small bronze balls between 2 moving steel parts for instance will reduce the friction between the surfaces, which reduces the wear on the steel parts.
Brass: Substitutional Alloy
Another way to make soft copper metal harder is to add zinc.
An alloy made up of copper and a smaller amount of zinc is known as brass.
Copper atoms and zinc atoms are of similar sizes:
| atom |
radius / Å |
radius / m |
radius ratio |
|
volume / m3 |
volume ratio |
|---|
| zinc |
1.20 |
1.20 × 10-10 |
0.98 |
|
7.24 × 10-30 |
0.95 |
| copper |
1.22 |
1.22 × 10-10 |
1 |
|
7.61 × 10-30 |
1 |
From the table we see that the radius of an atom of zinc is 0.98 times the radius of an atom of copper, that is, an atom of zinc has only a slightly smaller radius than a copper atom.
The volume of space occupied by an atom of zinc is 0.95 times the volume of space occupied by a copper atom, that is, the two atoms occupy a similar volume of space.
Zinc atoms can therefore substitute for some of the copper atoms in the metal lattice.
In the diagram on the right, copper atoms are shown as black circles, while the red circles represent atoms of zinc.
In the brass solid solution, copper is the solvent and zinc is the solute.
The composition of ordinary yellow brass is given below:
| Element |
% by mass |
m(element) = % × m(brass)
For 100 g sample of brass: |
|---|
| copper |
67 % |
67/100 × 100 = 67 g |
|---|
| zinc |
33 % |
33/100 × 100 = 33 g |
|---|
We can use this data to calculate the ratio of zinc to copper atoms in ordinary yellow brass:
|
m
/g |
Mr
/ g mol-1 |
n / mol
n = m ÷ Mr |
N / atoms
N = n × NA |
ratio of atoms |
|---|
| zinc |
33.00 |
65.38 |
33.00 ÷ 65.38 = 0.5047 |
0.5047 × 6.02 × 1023
= 3.04 × 1023 |
(3.04 × 1023) ÷ (3.04 × 1023)
= 1 |
|---|
| copper |
67.00 |
63.55 |
67.00 ÷ 63.55 = 1.0543 |
1.0543 × 6.02 × 1023
= 6.35 × 1023 |
(6.35 × 1023) ÷ (3.04 × 1023)
= 2.1 |
|---|
The ratio of zinc to copper atoms is approximately 1:2
That is, for 1 atom of zinc there are 2 atoms of cupper, or put another way, one-third of all the atoms in the lattice are zinc atoms while the other two-thirds are copper atoms.
We can estimate the impact this has on the density of the alloy by calculating the volume of space occupied by 33 g of zinc and 67 g of copper in the brass alloy:
| element |
density / g cm-3 |
mass / g |
volume / cm3
(= mass/density) |
|---|
| zinc |
7.13 |
33 |
33 ÷ 7.13 = 4.63 |
|---|
| copper |
8.96 |
67 |
67 ÷ 8.96 = 7.48 |
|---|
The density of the alloy can then be calculated:
| density of alloy = |
mass of alloy
volume of alloy |
| density of alloy = |
mass of copper + mass of zinc
volume of copper + volume of zinc |
| density of alloy = |
33 + 67
4.63 + 7.48 |
| density of alloy = |
100
12.11 |
| density of alloy = |
8.3 g cm-3 |
The density of ordinary yellow brass is inbetween that of zinc and copper.
We find there are other physical properties of the alloy, such as the melting point, which lie somewhere between the same property for each of the pure metals:
| Substance |
melting point / °C |
|---|
| zinc |
420 |
| copper |
1803 |
| brass |
900 |
By adding zinc to the copper lattice we have created an alloy that is less dense than copper, and has a lower melting point than copper which will make it easier to cast than copper.
Brass is more malleable than either zinc or bronze (an alloy of copper and tin) which means it can be hammered into sheets and bent into different shapes, making it ideal for use in musical instruments.
Pure copper metal is soft, pure zinc metal is also soft, but the brass alloy is harder than either copper or zinc.
Because brass is an attractive alloy with its bright, gold-like appearance, and because it has low metal-on-metal friction, it has been used in locks, gears, valves and ammunition casings.
1Alloys can be made up of more than 2 elements. A ternary alloy is made up of three elements, a quarternary alloy is made up of 4 elements, a quinary alloy is made up of 5 elements.
2A homogeneous metal solution will have the same crystal lattice structure as one the of the elements making up the alloy.
An alloy does not have to be homogeneous.
If the alloy has a crystal lattice that is different from crystal lattice of the elements making up the alloy then it is referred to as intermetallic.
If the alloy does not have a regular crystal structure at all, it is referred to as heterogeneous, for example, solder made up of about 50% lead and 50% tin is a heterogeneous alloy.
3The primary metal may also be referred to as the base or matrix.
4We are going to ignore the nature of this lattice during this discussion.
The representation given is for the most space-efficient packing of atoms in 2 dimensions.
5 Covalent radii are being used throughout this discussion.
Atomic radius is usually measured in angstroms (Å).
1 Å = 1 × 10-10m
6 Assuming atoms are spherical, V = 4/3πr3
7 We are assumuming additivity of volumes to perform this calculation.
