Electrorefining Chemistry Tutorial

Key Concepts

• Electrorefining refers to the process of using electrolysis to increase the purity of a metal extracted from its ore (compound or mixture of compounds from which a metal can be extracted commercially).

• The anode, positive electrode, is the impure metal to be purified.

  Oxidation, loss of electrons, occurs at the anode:

  For a metal, M

  M_(s) → Mⁿ⁺ + ne^-

• The cathode, negative electrode, is the electrode at which the pure metal will be deposited.

  Reduction, gain of electrons, occurs at the cathode.

  For a metal, M

  Mⁿ⁺ + ne^- → M_(s)

• The electrolyte is either a molten salt or an aqueous solution of the metal ions.
• Electrorefining can be used to purify a number of metals including copper, nickel, cobalt, lead and tin.

Electrorefining Copper

During the electrorefining stage of copper production, a series of impure copper anodes and thin starter sheet cathodes (such as thin copper foil) are suspended in a tank.

The electrolyte containing the copper ions flows through tank. The electrolyte is often copper dissolved in sulfuric acid which produces an aqueous solution of copper ions.

An external power supply is used to pull electrons out of the anode and push them to the cathode.

The animation below represents one of these electrolytic cells using an aqueous solution of Cu²⁺ as the electrolyte.

Anode (positive electrode) Impure copper plates. Oxidation occurs at the anode. Copper is oxidized at the anode. Cu(s) → Cu2+(aq) + 2e- Electrons are produced at the anode. Electrons flow from anode to cathode. Anode disintegrates. Copper ions migrate to cathode.

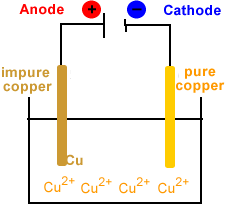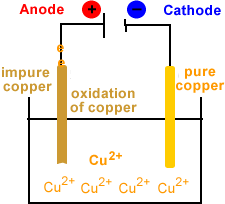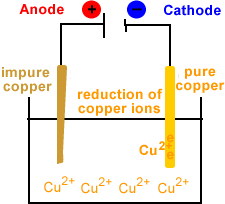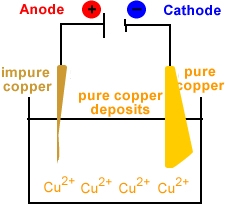Cathode (negative electrode) Starter sheets (thin copper foil or stainless steel blanks). Reduction occurs at the cathode. Copper ions migrate to the cathode. Copper ions are reduced at the cathode. Cu2+(aq) + 2e- → Cu(s) Solid copper is deposited at the cathode.

Note: H⁺ from the electrolyte is not reduced to H_2(g) at the cathode.
Cu²⁺ lies below H⁺ in the table of standard reduction potentials.
Cu²⁺ is a stronger oxidant than H⁺.
Cu²⁺ is more easily reduced than H⁺.

Some of the impurities that are found in the impure copper are silver, gold, and lead.

Each of these metals has commercial value so it is worthwhile collecting these from the tanks for purification.

Silver and gold occur below copper in the table of standard electrode potentials, so they are weaker reductants than copper and will not be oxidized at the anode. These will be found in the slime at the bottom of the tank.

Lead occurs above copper in the table of standard reduction potentials, so lead is a stronger reductant than copper and will be oxidized at the anode:

Pb_(s) → Pb²⁺_(aq) + 2e^-

However, lead forms an insoluble precipitate with the sulfate ions in the electrolyte:

Pb²⁺_(aq) + SO₄^2-_(aq) → PbSO_4(s)

PbSO_4(s) will be found in the slime at the bottom of the tank.