Dalton's Law of Partial Pressure of Gases Chemistry Tutorial

Key Concepts

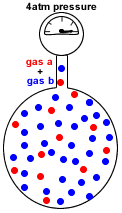
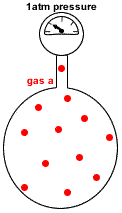
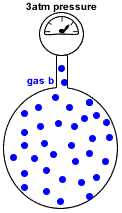
• Partial pressure of a gas in a mixture of gases is the pressure which that gas would exert if it were the only gas present in the container.
• Dalton's Law of Partial Pressures states that the total pressure in a gas mixture is the sum of the partial pressures of each individual gas:

  P_(total) = P_{(gas a)} + P_{(gas b)} + P_{(gas c)} + etc

  where:

  P_(total) = the total pressure exerted by the mixture of gases

  P_{(gas a)} = pressure exerted just by gas a

  P_{(gas b)} = pressure exerted just by gas b

  P_{(gas c)} = pressure exerted just by gas c

• Dalton's Law of Partial Pressures assumes each gas in the mixture is behaving like an ideal gas.

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Understanding Partial Pressure

Consider a container of fixed volume at constant temperature which holds a mixture of gas a and gas b at a total pressure of 4 atmospheres as shown in the diagram on the right. Pressure is caused by the gas molecules colliding with the walls of the container (Kinetic Theory of Gases). The total pressure in the container (P(total)) is proportional to the number of gas particles (N(total)): P(total) ∝ N(total) More gas particles leads to greater pressure. Less gas particles leads to lower pressure. If each dot represents 1 mole of gas particles, then there are 48 moles of gas particles in this container exerting a total pressure of 4 atm.
Now, imagine the container with no particles of gas b. Only particles of gas a are present in the same container at the same temperature, as shown in the diagram on the right. Now the container holds only 12 moles of gas particles instead of the 48 moles of gas particles it originally contained. Since pressure is proportional to the number of gas particles, we expect the pressure of gas a in the container to be less than 4 atm. the pressure exerted by gas a = 12 mol 48 mol × 4 atm   =   1   4 × 4 atm   = 1 atm We say that the pressure of gas a in this container is 1 atm. But, with reference to the original container containing a mixture of gas a and gas b, we say that the partial pressure of gas a in the mixture is 1 atm.
Now, imagine the container with no particles of gas a. Only particles of gas b are present in the same container at the same temperature as shown in the diagram on the right. Now the container holds only 36 moles of gas particles instead of the 48 moles of gas particles it originally contained. Since pressure is proportional to the number of gas particles, we expect the pressure to be less than 4 atm (the pressure of the mixture of gases in the original container). the pressure exerted by gas b = 36 mol 48 mol × 4 atm   =   3   4 × 4 atm   = 3 atm We say that the pressure of gas b in this container is 3 atm. But, with reference to the original container containing a mixture of gas a and gas b, we say that the partial pressure of gas b in the mixture is 3 atm.

Dalton's Law of Partial Pressures

Dalton's Law of Partial Pressures says that:

the total pressure in a gas mixture is the sum of the partial pressures of each individual gas

Using the example of the mixture of gas a and gas b in the previous section:

P(total)	=	P(gas a)	+	P(gas b)
	=		+

For an Ideal Gas, since gas pressure is directly proportional to the number of gas molecules (N) and there to moles of gas (n), we can also say that:

(i) P_(total) = (n_(total)RT) ÷ V (see Ideal Gas Law)

(ii) P_{(gas a)} = (n_{(gas a)} ÷ n_(total)) × P_(total)

(iii) P_{(gas b)} = (n_{(gas b)} ÷ n_(total)) × P_(total)

Dalton's Law of Partial Pressures Worked Example 1

Question : 10 g of nitrogen gas and 10 g of helium gas are placed together in a 10 L container at 25°C. Calculate the partial pressure of each gas in kPa and the total pressure in kPa of the gas mixture.

Solution:

(Based on the StoPGoPS approach to problem solving.)

1. What is the question asking you to do?

   Calculate partial pressure of each gas and total pressure
   P_{(nitrgen gas)} = ? atm
   P_{(helium gas)} = ? atm
   P_(total) = ? atm

2. What data (information) have you been given in the question?

   Extract the data from the question:

   m(nitrogen gas) = mass of nitrogen gas = 10 g
   m(helium gas) = mass of helium gas = 10 g
   V = volume of container = 10 L
   T = temperature of gas mixture = 25°C

3. What is the relationship between what you know and what you need to find out?

   Assume Ideal Gas behaviour

   (a) Ideal Gas Law: PV = nRT
   rearrange this equation to find the value of the total gas pressure of the mixture:
   

   P(total)

   =

   n(total)RT V

   (b) Pressure exerted by each gas is proportional to the number of molecules and hence to the moles of each gas.
   

   P(nitrogen gas)	=	n(nitrogen gas) n(total)	× P(total)
   P(helium gas)	=	n(helium gas) n(total)	× P(total)

4. (a) Calculate total gas pressure, P_(total)

   (i) Calculate moles of nitrogen gas:

   nitrogen is a diatomic gas with the molecular formula N₂

   moles(N₂) = mass(N₂) ÷ molar mass(N₂)
       mass(N₂) = 10 g (given in question)
       molar mass(N₂) = 2 × molar mass(N) = 2 × 14 = 28 g mol^-1
   moles(N₂) = 10 ÷ 28 = 0.357 mol

   (ii) Calculate moles of helium gas:

   helium is a monatomic gas with the molecular formula He

   moles(He) = mass(He) ÷ molar mass(He)
       mass(He) = 10 g (given in question)
       molar mass(He) = 4.0 g mol^-1 (from Periodic Table)
   moles(He) = 10 ÷ 4.0 = 2.50 mol

   (iii) Calculate total moles of gas in the mixture, n_(total):
   n_(total) = moles(N₂) + moles(He)
   n_(total) = 0.357 + 2.50 = 2.857 mol

   (iv) Calculate the total pressure of the gas mixture, P_(total)
   

   P(total)

   =

   n(total)RT V

   
   n_(total) = 2.857 mol (calculated above)
   R = gas constant = 8.314 J K^-1 mol^-1 (from Data Sheet)
   T = temperature in Kelvin = 273 + 25 = 298 K
   V = 10 L
   

   P(total)	=	2.857 × 8.314 × 298 10
   	=	7078 10
   	=	708 kPa

   (b) Calculate partial pressure of each gas, P_(nitrogen) and P_(helium)

   (i) Partial pressure of nitrogen gas:
   

   P(N2)	=	n(N2)   n(total)	× P(total)
   	=	0.357   2.857	× 708
   	=	0.125	× 708
   	=	88 kPa

   (ii) Partial pressure of helium gas:
   

   P(He)	=	n(He)   n(total)	× P(total)
   	=	2.50   2.857	× 708
   	=	0.875	× 708
   	=	620 kPa

5. Is your answer plausible?

   (a) Is the total pressure plausible?
   Molar volume of gas at 25°C and 100 kPa pressure is about 25 L
   About 3 moles of gas under the same conditions would have a volume of 3 × 25 = 75 L
   Given the volume of the container in the question is only 10 L, we expect the pressure in the container to about 75/10 × 100 kpa ≈ 750 kPa
   This result is in the same "ball park" as our carefully calculated value of 708 kPa we are reasonably confident that our answer is plausible.

   (b) The partial pressure of each gas must be less than the total pressure that was calculated for the mixture:
   P_(N2) = 88 kPa which is less than the P_(total) of 708 kPa.
   P_(He) = 620 kPa which is less than the P_(total) of 708 kPa.
   So our partial pressures look plausible.

   (c) Dalton's Law of Partial Pressures tells that:
   P_(total) = P_(N2) + P_(He) = 88 + 620 = 708 kPa
   That is, the sum of the partial pressure of each gas does add up to the total pressure of the gas mixture so our answer is plausible.

6. State your solution to the problem "partial pressure of each gas and total gas pressure":

   P_(N2(g)) = 88 kPa
   P_(He(g)) = 620 kPa
   P_(total) = 708 kPa

Dalton's Law of Partial Pressures Worked Example 2

Question : At 15°C, 25 mL of neon at 101.3 kPa (1atm) pressure and 75 mL of helium at 70.9 kPa (0.7 atm) pressure are both expanded into a 1 L sealed flask. Calculate the partial pressure of each gas in kPa and the total pressure of the gas mixture in kPa.

Solution:

(Based on the StoPGoPS approach to problem solving.)

1. What is the question asking you to do?

   Calculate partial pressure of each gas and total pressure
   P_{(neon gas)} = ? kPa
   P_{(helium gas)} = ? kPa
   P_(total) = ? kPa

2. What data (information) have you been given in the question?

   Extract the data from the question:

   T = temperature = constant = 15 °C

   V_{intial(neon gas)} = 25 mL = 25 mL ÷ 1000 mL/L = 0.025 L
   P_{intial(neon gas)} = 101.3 kPa

   V_{initial(helium gas)} = 75 mL = 75 mL ÷ 1000 mL/L = 0.075 L
   P_{intial(helium gas)} = 70.9 kPa

   V_{(final mixture)} = 1 L

3. What is the relationship between what you know and what you need to find out?

   Assume Ideal Gas behaviour: PV = nRT

   (a) For neon gas, moles of gas (n) and temperature (T) are constant, so
   P_(neon)V_(neon) = a constant (also see Boyle's Law)
   In other words:
   P_intial(neon)V_{initial(neon)} = P_final(neon)V_final(neon)
   which can be rearranged to calculate the final pressure due to neon gas:
   P_final(neon) = (P_intial(neon)V_{initial(neon)}) ÷ V_final(neon)

   (b) For helium gas, moles of gas (n) and temperature (T) are constant, so
   P_(helium)V_(helium) = a constant (also see Boyle's Law)
   In other words:
   P_{intial(helium)}V_{initial(helium)} = P_{final(helium)}V_{final(helium)}
   which can be rearranged to calculate the final pressure due to helium gas:
   P_{final(helium)} = (P_{intial(helium)}V_{initial(helium)}) ÷ V_{final(helium)}

   (c) Dalton's Law of Partial Pressure tells us that:
   P_(total) = P_final(neon) + P_{final(helium)}

4. (a) Calculate partial pressure of neon gas in gas mixture:

   P_final(neon) = (P_intial(neon)V_{initial(neon)}) ÷ V_final(neon)
   P_final(neon) = (101.3 × 0.025) ÷ 1 = 2.533 kPa = 2.5 kPa

   (b) Calculate partial pressure of helium gas in gas mixture:

   P_{final(helium)} = (P_{intial(helium)}V_{initial(helium)}) ÷ V_{final(helium)}
   P_{final(helium)} = (70.9 × 0.075) ÷ 1 = 5.3175 kPa = 5.3 kPa

   (c) Calculate total pressure of gas mixture in 1 L volume:

   P_final(total) = P_final(neon) + P_{final(helium)}
   P_final(total) = 2.5 + 5.3 = 7.8 kPa

5. Is your answer plausible?

   (a) Calculate moles of neon gas:
   n(Ne) = (PV) ÷ (RT)
   n(Ne) = (101.3 × 0.025) ÷ (8.314 × 288) = 1.06 × 10^-3 mol

   (b) Calculate moles of helium gas:
   n(He) = (PV) ÷ (RT)
   n(He) = (70.9 × 0.075) ÷ (8.314 × 288) = 2.22 × 10^-3 mol

   (c) Calculate total gas pressure in mixture:
   PV = n_(total)RT
   P_(total)V = [n(Ne) + n(He)]RT
   P_(total) = ([n(Ne) + n(He)]RT) ÷ V = ([1.06 × 10^-3 + 2.22 × 10^-3] × 8.314 × 288) ÷ 1 = 7.8 kPa

   
   There is good agreement between the total pressure we calculated above and this new calculation, so we are reasonably confident our answer is plausible.

6. State your solution to the problem "partial pressure of each gas and total gas pressure":

   P_{(neon gas)} = 2.5 kPa
   P_{(helium gas)} = 5.3 kPa
   P_(total) = 7.8 kPa