Polystyrene Chemistry Tutorial

Key Concepts

• Polystyrene is also known as poly(ethenylbenzene), poly(phenylethene), poly(1-phenylethene), poly(1-phenylethane-1,2-diyl) ¹.
• Polystyrene can be produced in an addition polymerisation reaction.
• The monomer used in the addition polymerisation reaction has the systematic IUPAC name of ethenylbenzene.
  Ethenylbenzene is also known as phenylethene, vinyl benzene, or as styrene.
  Ethenylbenzene (phenylethene or styrene) is a colourless, oily liquid hydrocarbon produced from petrochemicals.
• Polystyrene forms a transparent plastic which is used for plastic containers, plastic knives, forks and spoons.
• Gas can be added to polystyrene during production to make expanded polystyrene or polystyrene foam (styrofoam™²) which is used as heat insulation in things like coffee cups.
  This polystyrene foam, or expanded polystyrene (EPS), has a low density so can be used to make flotation devices, and in packaging like peanut shaped loose packaging, trays and boxes.
• Polystyrene is a thermoplastic polymer, that is, it softens on heating so it can be molded into different shapes then cooled to become hard again.
  It is therefore possible to recycle polystyrene.³
• Polystyrene is chemically inert, resistant to acids and bases, but is soluble in many chlorinated solvents.
  Polystyrene is very slow to biodegrade.
• Polystyrene is flammable, usually underdoing incomplete combustion resulting in a sooty flame.

Addition Polymerisation Reaction

styrene	→	polystyrene
H |   | n C = C | H   | H	→	H | | H | | H | | H | | H | | H | | H | | -[ - C - C - C - C - C - C - C - C - C - C - C - C - C - C - ]n- | H | H | H | H | H | H | H | H | H | H | H | H | H | H

By Le Chatelier's Principle, increasing the temperature at which the reaction occurs would favour the reactant, monomer, side of the equation. The addition polymerisation reaction is therefore carried out at very mild temperatures.

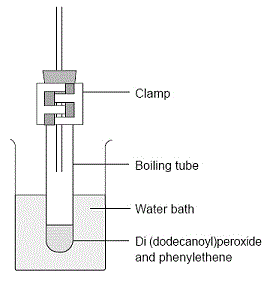
Polystyrene can be produced in the school laboratory as a demonstration.

Set up a water bath using a 250 mL of boiling water. Add 0.1 g of di(dodecanoyl) peroxide to 5 mL of styrene4 in a boiling tube. Insert 20 cm of glass tubing through a rubber bung (stopper) and position the rubber bung in the neck of the flask as shown in the diagram. This minimises the loss of escaping styrene vapour during heating. Position the boiling tube so that the level of the solution in it is below the level of the hot water and clamp it in place. Heat for 30 minutes until the solution becomes viscous. Extinguish all flames and remove the boiling tube from the water bath and cool. Pour the contents of the cooled boiling tube into 50 mL of ethanol in a beaker. Push the polystyrene into a lump using a glass rod. Pour off the ethanol. Dry the solid polystyrene on filter paper.

Safety Considerations Wear eye protection (safety glasses or goggles) and disposable gloves. Styrene vapour is narcotic at high concentrations, Work in a fume cupboard, or, ensure good ventilation. Styrene is flammable, keep clear of flames. Di(dodecanoyl) peroxide (lauroyl peroxide) is an oxidising agent, avoid contact with skin, benches etc. Ethanol is flammable, keep clear of flames. Polystyrene is flammable, keep clear of flames.

You could test the solubility of your polystyrene in various solvents such as concentrated hydrochloric acid (12 mol L^-1), dilute hydrochloric acid (10% HCl(aq)), cyclohexane, olive oil, dichloromethane, bromine and 2-butanone.

Reaction Mechanism

The addition polymerisation of styrene (ethenylbenzene or phenylethene) to produce polystyrene (poly(phenylethene) or poly(ethenylbenzene)) proceeds by a free-radical mechanism.
A free radical is a molecule that has no charge, but, is highly reactive because it has an unpaired valence electron.
Di(dodecanoyl) peroxide can be used as an initiator for the polymerisation reaction because it has a peroxy group (-O-O-) between two large dodecanoyl groups (CH₃(CH₂)₁₀CO-).
The peroxy O-O bond breaks readily, splitting the di(dodecanoyl)peroxide molecule into two, and leaving unpaired electrons on the oxygen atoms.
This results in the formation of the free radical CH₃(CH₂)₁₀COO^.

Initiation: free radical initiator attacks the styrene monomer, opening the double bond and producing a new free radical with an unpaired electron on a carbon atom

R.

+

H |   | C = C | H   | H

→

H |   | R- C - C. | H   | H

Propagation: the new free radical produced during initiation can then react with a styrene molecule, opening up the double bond and leaving an unpaired electron on a carbon atom

H |   | R- C - C. | H   | H

+

H |   | C = C | H   | H

→

H |   |   H |   |   R- C - C - C - C.         etc | H   | H   | H   | H

Termination: polymerisation stops when two free radicals react with each other

R.

+

H |   |   H |   |   R- C - C - C - C.   | H   | H   | H   | H

→

H |   |   H |   |   R- C - C - C - C -R | H   | H   | H   | H

Structure of Polystyrene

1. All the styrene molecules combine so that the benzene rings () are all on the same side of the carbon backbone of the polymer chains:

H |

|

H |

|

H |

|

H |

|

H |

|

H |

|

H |

|

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

| H

| H

| H

| H

| H

| H

| H

| H

| H

| H

| H

| H

| H

| H

This structure is known as isotactic polystyrene.

The regular arrangement of the benzene rings in this structure allows the polymer chains to pack together closely and maximises the intermolecular forces between the chains. Close packing reduces the flexibility of the material, so isotactic polystyrene would be quite rigid, and because the intermolecular forces between polymer chains is maximised, it would also be quite strong. Isotactic polystyrene is said to be highly crystalline.

Although we commonly like to draw the structure of polystyrene as the isotactic structure because it is easy to see the repeating units, in fact, when styrene monomers are polymerised very little of the resulting polystyrene is in the isotactic form.

2. The styrene (ethenylbenzene or phenylethene) molecules combine so that the benzene rings () alternate between being above the plane of the carbon backbone and being below it:

H |

H |

H |

|

H |

H |

H |

|

H |

H |

H |

|

H |

H |

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

| H

|

| H

| H

| H

|

| H

| H

| H

|

| H

| H

| H

|

This structure is known as syndiotactic polystyrene.

The regular arrangement of the benzene rings in this structure allows the polymer chains to pack together closely and be held in place by intermolecular forces between the chains. Close packing reduces the flexibility of the material, so syndiotactic polystyrene is quite rigid, and the action of intermolecular forces between polymer chains makes it quite strong. Syndiotactic polystyrene, like isotactic polystyrene, is said to be highly crystalline.
Very little of the polystyrene produced by the addition polymerisation of styrene (ethenylbenzene or phenylethene) is syndiotactic polystyrene.
However, Chemists think syndiotactic polystyrene could be used to make medical equipment because it is able to withstand the heat, moisture and cleaners used to sterilize medical equipment, but it is currently quite expensive to produce.

3. The styrene (ethenylbenzene or phenylethene) molecules combine so that benzene rings () are randomly oriented along the chains, with some above and some below the plane of the carbon backbone:

H |

H |

H |

|

H |

|

H |

|

H |

H |

H |

|

H |

H |

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

C

-

| H

|

| H

| H

| H

| H

| H

| H

| H

|

| H

| H

| H

|

This structure is known as atactic polystyrene.

The large benzene rings sticking out at random along the chains prevent the polymer chains from packing together closely. Atactic polystyrene is not crystalline, rather, it is said to be amorphous. Non-crystalline or amorphous polymers are expected to be softer and more flexible.

Most of the polystyrene produced by the addition polymerisation of styrene is atactic polystyrene.
Atactic polystyrene is the polystyrene you will find in polystyrene containers, cases, cups, plastic cultery etc.

Properties and Uses of Polystyrene

Polystyrene is a linear polymer, and, like most linear polymers, the application of heat and pressure will cause it soften and take on new shapes. These linear polymers are said to be thermoplastic. Polystyrene is a thermoplastic.

⁴Styrene, or ethenylbenzene or phenylethene, may contain the inhibitor 4-(dimethylethyl)-benzene-1,2-diol (4-tert-butyl catechol) which needs to be removed by washing with 1 mol L^-1 NaOH(aq) then with water in a separating funnel. Dry the phenylethene over anhydrous sodium sulfate, Na₂SO₄(s), for 10 minutes. Wash all equipment in propanone (acetone), CH₃COCH₃.