Enthalpy of Neutralisation or Heat of Neutralization Chemistry Tutorial
Key Concepts
⚛ Neutralisation, or neutralization, is the name given to the reaction that occurs between an Arrhenius acid and an Arrhenius base. (1)
H+(aq) + OH-(aq) → H2O(l)
⚛ When an acid is added to an aqueous solution of base, the temperature of the solution increases.
Or, if a base is added to an aqueous solution of an acid, the temperature of the solution increases.
⚛ Energy (heat) is produced when an acid reacts with a base in a neutralisation reaction.
· Neutralisation reactions are exothermic.
· ΔH for a neutralisation reaction is negative.
⚛ Molar enthalpy of neutralisation (molar heat of neutralization) is the energy liberated per mole of water formed during a neutralisation reaction.
· ΔneutH (or ΔHneut) is the symbol given to the molar enthalpy of neutralisation. (2)
· ΔneutH is usually given in units of kJ mol-1
(kJ of energy released per mole of water produced)
⚛ Enthalpy of neutralisation can be determined in the school laboratory using a styrofoam™ cup solution calorimter(3). Calculating the molar enthalpy of neutralisation from experimental results is a 3 step process:
Step 1: Calculate the heat evolved: q = m × Cg × ΔT
m = total mass of reaction mixture
Cg = specific heat capacity of solution
ΔT = change in temperature of solution
Step 2: Calculate the enthalpy change for the reaction: ΔH = −q
Step 3: Calculate the molar enthalpy of neutralisation: ΔneutH = ΔH ÷ n(H2O(l))
⚛ Molar enthalpy of neutralisation for reactions between dilute aqueous solutions of strong acid and strong base is always the same(4), that is,
ΔneutH = -55.90 kJ mol -1
because no bonds need to be broken, and because making the H-O bonds in H2O releases energy
(breaking bonds is an endothermic process, making bonds is an exothermic process)
⚛ Less than 55.90 kJ mol-1 of energy is released when:
(a) a weak acid neutralises a strong base
(b) a strong acid neutralises a weak base
(c) a weak acid neutralises a weak base
because some of the energy is consumed in the process of breaking weak acid bonds and/or weak base bonds.
Please do not block ads on this website.
No ads = no money for us = no free stuff for you!
Polstyrene Cup Calorimeter for Enthalpy of Neutralisation Experiment
Expanded polystyrene (polystyrene foam or styrofoam™) cups are often used as take-away coffee cups because the expanded polystyrene is a good insulator, that is, your coffee stays hot but you don't burn your fingers holding the cup!
This same insulating property can be exploited to make a reasonably good calorimeter (a device used to measure energy, or heat, change during a chemical reaction).
A schematic diagram of a simple polystyrene foam cup calorimeter is shown below:
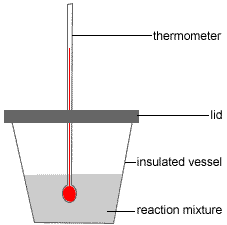
A known amount of a reactant, such as a dilute aqueous solution of a base, is placed in the polystyrene cup (insulated vessel in the diagram).
The following data for this solution are recorded:
concentration: c1 = ? mol L-1
volume = V1 = ? mL
A small hole is placed in the polystyrene lid to allow a thermometer to be pushed through. The fit must be snug enough to hold the thermometer in place, suspended off the bottom of the cup and immersed in the reactant.
It is assumed no heat will be lost through the lid or the hole in the lid.
The intial temperature of the reactant is measured and recorded.
initial temperature = Ti = ? °C
A known amount of the second reactant, for example a dilute solution of acid, at the same temperature is added to the solution in the cup.
The following data for this second solution are recorded:
concentration: c2 = ? mol L-1
volume = V2 = ? mL
The thermometer is also used to stir the solution while the reaction is taking place.
The temperature of the solution in the cup will rise.
The maximum temperature reached is recorded as the final temperature.
final temperature = Tf = ? °C
For the calculation of heat of neutralization (enthalpy of neutralisation) we need to determine:
(i) total mass, m, of the solution in the cup
First assume additivity of volumes so that total volume of solution, Vf, is the sum of the volume of the two reactants:
Vf = V1 + V2
Then assume that, because all of the solutions are dilute aqueous solutions, the density of each solution and hence the density of the final solution, d, is the same as water which we will assume is 1.00 g mL-1
density = mass (g) ÷ volume (mL)
Substitute the density of water into the equation:
1.00 (g/mL) = mass (g) ÷ Vf (mL)
Multiplying both sides of the equation by Vf (mL)
Vf (mL) × 1.00 (g/mL) = Vf (mL) × mass (g) ÷ Vf (mL)
Vf × 1.00 = mass (g) = m g
(ii) specific heat capacity, Cg, of the solution
Assume that, because all of the solutions are dilute aqueous solutions, the specific heat capacity of each solution and hence the specific heat capacity of the final solution, Cg, is the same as water which we will assume is 4.18 J g-1 °C-1
Cg = 4.18 J g-1 °C-1
(iii) change in temperature, ΔT, as a result of the neutralisation reaction:
ΔT = (Tf − Ti) °C
Now we can calculate the heat released by this neutralisation reaction, q,
q = m × Cg × ΔT
In order to determine the molar enthalpy of neutralisation (molar heat of neutralization), we need to determine how many moles of water, n(H2O(l)), have been formed as a result of the reaction:
H+(aq) + OH-(aq) → H2O(l)
So, using the stoichiometric ratio (mole ratio), we can see that:
n(H+(aq)) = n(OH-(aq)) = n(H2O(l))
Now we can calculate the energy released per mole of water, or the molar enthaply of neutralisation (molar heat of neutralization), ΔneutH
Remember, the reaction is exothermic so the sign of ΔH will be negative!
ΔneutH = −q ÷ n(H2O(l))
↪ Back to top
Enthalpy of Neutralisation: Strong Monoprotic Acid + Strong Monobasic Base
HCl(aq) is a strong monoprotic acid, it completely dissociates (ionises) in water to produce hydrogen ions (H+(aq)) and chloride ions (Cl-(aq)):
HCl(aq) → H+(aq) + Cl-(aq)
n(HCl(aq)) : n(H+(aq)) is 1:1 (that is, monoprotic)
NaOH(aq) is a strong monobasic base, it completely dissociates (ionises) in water to produce sodium ions (Na+(aq)) and hydroxide ions (OH-(aq)):
NaOH(aq) → Na+(aq) + OH-(aq)
n(NaOH(aq)) : n(OH-(aq)) is 1:1 (that is, monobasic)
A neutralization reaction occurs when HCl(aq) is added to NaOH(aq)
HCl(aq) + NaOH(aq) → H2O(l) + NaCl(aq)
and heat energy is given off (the reaction is said to be exothermic)
In an experiment to determine the molar enthalpy of neutralisation, 50.0 mL of 1.00 mol L-1 NaOH(aq) is placed in the styrofoam cup.
The temperature of the NaOH(aq) is recorded.
1.00 mol L-1 HCl(aq) at the same temperature is added 10.0 mL at a time.
The reaction mixture is stirred between each addition.
The maximum temperature the solution reached is then recorded.
The results of the experiment are shown in the table below:
total volume HCl(aq)
added (mL) | temperature in
calorimeter (°C) |
|---|
| 0 | 18.0 |
| 10 | 20.2 |
| 20 | 21.8 |
| 30 | 22.9 |
| 40 | 23.8 |
| 50 | 24.6 |
| 60 | 24.0 |
| 70 | 23.6 |
and the results have been plotted on the graph shown below:
temperature (°C) |
HCl(aq) added to NaOH(aq)
total volume of
HCl(aq) added (mL) |
Initially, the temperature of the reaction mixture in the calorimeter (styrofoam™ cup) increases as HCl(aq) is added.
Energy (heat) is being produced by the reaction.
The reaction is exothermic.
Maximum temperature reached is 24.6°C when 50.0 mL of HCl(aq) had been added.
When 50.0 mL of the acid has been added, all the base has been neutralised.
HCl(aq) + NaOH(aq) → NaCl(aq) + H2O(l)
moles HCl(aq) added = moles of NaOH(aq) present in the calorimeter
Adding more acid doesn't increase the temperature in the calorimeter any further(5).
We can calculate the molar enthalpy of neutralisation (molar heat of neutralization) for the reaction if we assume that the:
(i) density of each dilute aqueous solution is the same as water, 1 g mL-1 at 25°C
so, the mass of solution in grams = volume of solution in mL
(ii) heat capacity of each solution is the same as for water, Cg = 4.18 J°C-1g-1
Calculating the molar enthalpy of neutralisation using the data from the experiment:
Step 1: Extract the data needed to calculate the molar heat of neutralisation for this reaction:
V(NaOH) = volume of NaOH(aq) in the calorimeter = 50.0 mL
V(HCl) = volume of HCl(aq) added to achieve neutralisation = 50.0 mL
c(NaOH) = concentration of NaOH(aq) = 1.00 mol L-1
c(HCl) = concentration of HCl(aq) = 1.00 mol L-1
Ti = initial temperature of solutions before additions = 18.0°C
Tf = final temperature of solution at neutralisation = 24.6°C
d = density of solutions = 1 g mL-1 (assumed)
Cg = specific heat capacity of solutions = 4.18 J°C-1g-1 (assumed)
q = heat liberated during neutralisation reaction = ? J
Step 2: Check the units for consistency and convert if necessary:
Convert volume of solutions (mL) to mass (g):
density × volume = mass
since density = 1 g mL-1:
1 × volume (mL) = mass (g)
mass(NaOH) = 50.0 g
mass(HCl) = 50.0 g
Step 3: Calculate the heat produced during the neutralisation reaction:
heat produced = total mass × specific heat capacity × change in temperature
q = mtotal × Cg × ΔT
mtotal = mass(NaOH) + mass(HCl) = 50.0 + 50.0 = 100.0 g
Cg = 4.18 J°C-1g-1
ΔT = Tf - Ti = 24.6 - 18.0 = 6.6°C
q = 100.0 g × 4.18 J g-1 °C-1 × 6.6 °C = 2758.8 J
Step 4: Calculate the moles of water produced:
OH-(aq) + H+(aq) → H2O(l)
1 mol OH-(aq) + 1 mol H+(aq) → 1 mol H2O
moles(H2O) = moles(OH-(aq))
moles(OH-(aq)) = concentration (mol L-1) × volume (L)
= 1.0 mol L-1 × 50.0 mL/1000 mL/L = 0.050 mol
moles of water produced = 0.050 mol
Step 5: Calculate the heat liberated per mole of water produced, ΔneutH :
ΔneutH will be negative because the reaction is exothermic
ΔneutH = heat liberated per mole of water
= -1 × q ÷ moles of water
ΔneutH = -1 × 2758.8 J ÷ 0.050 mol
= -55176.0 J mol-1
We can convert J to kJ by dividing by 1000:
ΔneutH = -55176.0 J mol-1 ÷ 1000 J/kJ = 55.2 kJ mol-1
↪ Back to top
Enthalpy of Neutralisation: Strong Diprotic Acid and Strong Monobasic Base
The experiment described above is repeated using 50.0 mL of 1.00 mol L-1 sodium hydroxide, a strong monobasic base, and 1.00 mol L-1 sulfuric acid, a strong diprotic acid, instead of 1.00 mol L-1 hydrochloric acid, a strong monoprotic acid.
When plotted on a graph as shown below, the second experiment's results look different when compared to the first experiment's results:
temperature (°C) |
Acid + NaOH
total volume of acid added (mL) |
Initially, the temperature of the reaction mixture in both experiments increases as acid is added.
Energy (heat) is being produced by the reaction. The reaction is exothermic.
Maximum temperature reached for the reaction with H2SO4(aq) is higher than the maximum temperature reached for the reaction with HCl(aq).
Volume of H2SO(aq) added to reach the maximum temperature is less than the volume of HCl(aq) needed to reach maximum temperature.
For the reaction HCl(aq) + NaOH(aq) → NaCl(aq) + H2O(l)
we found that ΔneutH = -55.2 kJ mol-1 (per mole of water formed)
So, H+(aq) + OH- → H2O(l) ΔneutH = -55.2 kJ mol-1
For the reaction H2SO4(aq) + 2NaOH(aq) → Na2SO4(aq) + 2H2O(l)
2H+(aq) + 2OH-(aq) → 2H2O(l)
so, H+(aq) + OH-(aq) → H2O(l)
We predict that ΔneutH = -55.2 kJ mol-1
We can use the results of the second experiment to calculate the value for the molar enthalpy of neutralisation (ΔneutH), and see if they agree with our prediction.
Calculate the molar heat of neutralisation for the reaction from the results of the experiment shown in the graph above:
H2SO4(aq) + 2NaOH(aq) → Na2SO4(aq) + 2H2O(l)
Step 1: Extract the data needed to calculate the molar heat of neutralisation for this reaction:
V(NaOH) = volume of NaOH(aq) in the calorimeter = 50.0 mL
V(H2SO4) = volume of H2SO4(aq) added to achieve neutralisation = 25.0 mL
c(NaOH) = concentration of NaOH(aq) = 1.00 mol L-1
c(H2SO4) = concentration of H2SO4(aq) = 1.00 mol L-1
Ti = initial temperature of solutions before additions = 18.0°C
Tf = final temperature of solution at neutralisation = 26.9°C
d = density of solutions = 1 g mL-1 (assumed)
Cg = specific heat capacity of solutions = 4.18 J°C-1g-1 (assumed)
q = heat liberated during neutralisation reaction = ? J
Step 2: Check the units for consistency and convert if necessary:
Convert volume of solutions (mL) to mass (g):
density × volume = mass
since density = 1 g mL-1:
1 × volume (mL) = mass (g)
mass(NaOH) = 50.0 g
mass(H2SO4) = 25.0 g
Step 3: Calculate the heat produced during the neutralisation reaction:
heat produced = total mass × specific heat capacity × change in temperature
q = mtotal × Cg × ΔT
mtotal = mass(NaOH) + mass(H2SO4() = 50.0 + 25.0 = 75.0 g
Cg = 4.18 J°C-1g-1
ΔT = Tf - Ti = 26.9 - 18.0 = 8.9°C
q = 75.0 g × 4.18 J g-1 °C × 8.9 °C = 2790.2 J
Step 4: Calculate the moles of water produced:
OH-(aq) + H+(aq) → H2O(l)
1 mol OH-(aq) + 1 mol H+(aq) → 1 mol H2O
moles(H2O) = moles(OH-(aq))
moles(OH-(aq)) = concentration (mol L-1) × volume (L)
= 1.0 × 50.0/1000
= 0.050 mol
moles of water produced = 0.050 mol
Step 5: Calculate the heat liberated per mole of water produced, ΔneutH :
ΔneutH will be negative because the reaction is exothermic
ΔneutH = heat liberated per mole of water
= -1 × q ÷ moles of water
ΔneutH = -1 × 2790.2 J ÷ 0.050 mol
= -55803 J mol-1 (of water produced)
We can divide J by 1000 to convert this enthalpy change to kJ per mole:
ΔneutH = -55803 J mol-1 ÷ 1000 J/kJ
= -55.8 kJ mol-1 (of water produced)
Now compare the molar enthalpy of neutralisation (molar heat of neutralization) for:
| HCl(aq) + NaOH(aq) → NaCl(aq) + H2O(l) | ΔneutH = -55.2 kJ mol-1 (of water) |
| H2SO4(aq) + 2NaOH(aq) → Na2SO4(aq) + 2H2O(l) | ΔneutH = -55.8 kJ mol-1 (of water) |
There is close agreement between the two values for molar heat of neutralisation, so we can generalise and say that the molar enthalpy of neutralisation for the reaction between a strong acid and a strong base is a constant.
↪ Back to top
Molar Enthalpy of Neutralisation: Weak Acid + Strong Base
The experiment described above is repeated using 50.0 mL of 1.00 mol L-1 sodium hydroxide, a strong monobasic base, and 1.00 mol L-1 aqueous hydrogren cyanide (HCN(aq), hydrocyanic acid or prussic acid), a weak monoprotic acid (Ka ≈ 6 × 10-10), instead of 1.00 mol L-1 hydrochloric acid, a strong monoprotic acid.
The results of these experiments are shown in the graph below:
temperature (°C) |
Acid + NaOH
total volume of acid added (mL) |
Initially, the temperature of the reaction mixture in both experiments increases as acid is added.
Energy (heat) is being produced by the reaction. The reaction is exothermic.
Maximum temperature reached for the reaction with HCN(aq) is much less than the maximum temperature reached for the reaction with HCl(aq).
Volume of HCN(aq) added to reach the maximum temperature is the same as the volume of HCl(aq) needed to reach maximum temperature (both volumes are 50.0 mL).
For the reaction HCl(aq) + NaOH(aq) → NaCl(aq) + H2O(l)
we found that ΔneutH = -55.2 kJ mol-1 (per mole of water formed)
So, H+(aq) + OH- → H2O(l) ΔneutH = -55.2 kJ mol-1
For the reaction HCN(aq) + NaOH(aq) → NaCN(aq) + H2O(l)
Will ΔneutH for this reaction be the same (-55.2 kJ mol-1) ?
We can use the results of the HCN experiment recorded in the graph above to calculate the value for the molar enthalpy of neutralisation (ΔneutH), and see.
Step 1: Extract the data needed to calculate the molar heat of neutralisation for this reaction:
V(NaOH) = volume of NaOH(aq) in the calorimeter = 50.0 mL
V(HCN) = volume of HCN(aq) added to achieve neutralisation = 50.0 mL
c(NaOH) = concentration of NaOH(aq) = 1.00 mol L-1
c(HCN) = concentration of HCN(aq) = 1.00 mol L-1
Ti = initial temperature of solutions before additions = 18.0°C
Tf = final temperature of solution at neutralisation = 19.2°C
d = density of solutions = 1 g mL-1 (assumed)
Cg = specific heat capacity of solutions = 4.18 J°C-1g-1 (assumed)
q = heat liberated during neutralisation reaction = ? J
Step 2: Check the units for consistency and convert if necessary:
Convert volume of solutions (mL) to mass (g):
density × volume = mass
since density = 1 g mL-1 (assumed):
1 × volume (mL) = mass (g)
mass(NaOH) = 50.0 g
mass(HCN) = 50.0 g
Step 3: Calculate the heat produced during the neutralisation reaction:
heat produced = total mass × specific heat capacity × change in temperature
q = mtotal × Cg × ΔT
mtotal = mass(NaOH) + mass(HCN) = 50.0 + 50.0 = 100.0 g
Cg = 4.18 J°C-1g-1
ΔT = Tf - Ti = 19.2 - 18.0 = 1.2°C
q = 100.0 g × 4.18 J g-1 °C-1 × 1.2 °C = 501.6 J
Step 4: Calculate the moles of water produced:
NaOH(aq) + HCN(aq) → NaCN(aq) + H2O(l)
moles(H2O) = moles(NaOH)
moles(NaOH(aq)) = concentration (mol L-1) × volume (L)
= 1.0 mol L-1 × 50.0 mL/1000 mL/L = 0.050 mol
moles of water produced = 0.050 mol
Step 5: Calculate the heat liberated per mole of water produced, ΔneutH :
ΔneutH will be negative because the reaction is exothermic
ΔneutH = heat liberated per mole of water
= -1 × q ÷ moles of water
ΔneutH = -1 × 501.6 ÷ 0.050
= -10032 J mol-1
We can convert J to kJ by dividing by 1000:
ΔneutH = -10032 J mol-1 ÷ 1000 J/kJ
= -10.0 kJ mol-1
Compare the molar heat of neutralisation for the neuralisation of NaOH(aq) by both HCl(aq) and HCN(aq):
| HCl(aq) + NaOH(aq) → NaCl(aq) + H2O(l) | ΔneutH = -55.2 kJ mol-1 (of water) |
| HCN(aq) + NaOH(aq) → NaCN(aq) + H2O(l) | ΔneutH = -10.0 kJ mol-1 (of water) |
The heat released per mole of water for the HCN(aq) reaction is much less than the heat released per mole of water for the HCl(aq) reaction.
The difference in molar enthalpy of neutralisation is due to the type of reaction taking place:
(i) Strong Acid + Strong Base Reaction:
⚛ Strong base, NaOH, fully dissociates in water. The reacting species is OH-(aq)
⚛ Strong acid, HCl, fully dissociates in water. The reacting species is H+(aq)
⚛ The reaction is therefore an Arrhenius neutralisation reaction:
H+(aq) + OH-(aq) → H2O(l)
⚛ No bonds need to broken in the strong acid or strong base, no energy is lost in breaking bonds.
⚛ Energy is released when the H-O bonds form in the H2O product.
(ii) Weak Acid + Strong Base
⚛ Strong base, NaOH, fully dissociates in water. The reacting species is OH-(aq)
⚛ Weak acid, HCN(aq), only partially dissociates in water.
Most of the acid species in solution are undissociated HCN molecules.
⚛ The reaction is therefore a Brønsted-Lowry proton transfer reaction:
HCN(aq) + OH-(aq) → CN-(aq) + H2O(l)
⚛ In order for this reaction to occur, H-C bonds in HCN molecules must be broken before H2O molecules can be produced.
Breaking covalent bonds is an endothermic reaction, it absorbs energy.
⚛ So, even though we might expect the same amount of energy to be produced in both the HCl(aq) and HCN(aq) reactions because both reactions are producing the same number of moles of H2O, we see that energy will be consumed in breaking bonds in HCN so the amount of energy produced overall will be less than that for the HCl + NaOH reaction.
The heat liberated per mole when a weak acid neutralises a strong base is less than the amount of heat liberated per mole when a strong acid neutralises a strong base.
↪ Back to top
Problem Solving: Molar Enthalpy of Neutralisation
The Problem: The heat released when an aqueous solution of acetic acid reacted with aqueous sodium hydroxide was measured in the laboratory using a cup calorimeter.
The calorimeter consisted of two styrofoam™ coffee cups, one inside the other.
This was covered with a styrofoam™ lid through which a thermometer and a stirring rod were placed.
The two reacting aqueous solutions, acetic acid and sodium hydroxide, were placed in the inner cup.
The following data were obtained:
| Volume of 1.0 mol L-1 CH3COOH(aq) used | = | 50.0 mL |
| Volume of 1.0 mol L-1 NaOH(aq) used | = | 50.0 mL |
| Initial temperature of CH3COOH(aq) | = | 25.0 °C |
| Initial temperature of NaOH(aq) | = | 25.2 °C |
| Maximum temperature of mixture | = | 31.0 °C |
| Heat capacity of water and of the mixture | = | 4.18 J g-1°C-1 |
Determine the molar enthalpy of neutralisation for this reaction in kJ mol-1.
Solving the Problem using the StoPGoPS model for problem solving:
| STOP! |
State the question. |
What is the question asking you to do?
Determine (calculate) the molar enthalpy of neutralisation in kJ mol-1
ΔneutH = ? kJ mol-1
|
| PAUSE! |
Pause to Plan. |
What information (data) have you been given?
c(CH3COOH(aq)) = 1.0 mol L-1
V(CH3COOH(aq)) = 50.0 mL
c(NaOH(aq)) = 1.0 mol L-1
V(NaOH(aq)) = 50.0 mL
Ti(CH3COOH(aq)) = 25.0 °C
Ti(NaOH(aq)) = 25.2 °C
Tf = 31.0 °C
Cg = 4.18 J g-1°C-1
What is your plan for solving this problem?
Step 1: Calculate the heat produced, q, in J :
q = m(total) × Cg × ΔT
Step 2: Calculate the enthalpy change for the reaction, ΔH, in J :
ΔH = −q
Step 3: Calculate the heat produced per mole of water produced, ΔneutH, in J mol-1 :
ΔneutH = ΔH ÷ n(H2O(l))
Step 4: Convert J mol-1 to kJ mol-1
ΔneutH kJ mol-1 = ΔneutH J mol-1 ÷ 1000 J/kJ
|
| GO! |
Go with the Plan. |
Step 1: Calculate the heat produced, q, in J :
q = m(total) × Cg × ΔT
V(total) = V(CH3COOH(aq)) + V(NaOH(aq)) = 50.0 + 50.0 = 100.0 mL
assume density of mixture = 1.0 g mL-1, then
m(total) = 100.0 g
Cg = 4.18 J g-1 °C-1
Ti(mixture) = [Ti(CH3COOH(aq)) + Ti(NaOH(aq))] ÷ 2 = [25.0 + 25.2]/2 = 25.1 °C
Tf(mixture) = 31.0 °C
ΔI(mixture) = 31.0 − 25.1 = 5.9 °C
q = 100.0 × 4.18 × 5.9 = 2466.2 J
Step 2: Calculate the enthalpy change for the reaction, ΔH, in J :
ΔH = −q = −2466.2 J
Step 3: Calculate the heat produced per mole of water produced, ΔneutH, in J mol-1 :
ΔneutH = ΔH ÷ n(H2O(l))
CH3COOH(aq) + NaOH(aq) → CH3COONa(aq) + H2O(l)
n(H2O(l)) = n(CH3COOH(aq)) = c × V = 1.0 mol L-1 × 50.0 mL/1000 mL/L = 0.050 mol
ΔneutH = −2466.2 J ÷ 0.050 mol = −49324 J mol-1
Step 4: Convert J mol-1 to kJ mol-1
ΔneutH kJ mol-1 = ΔneutH J mol-1 ÷ 1000 J/kJ
ΔneutH kJ mol-1 = −49324 J mol-1 ÷ 1000 J/kJ = −49 kJ mol-1
(Only 2 significant figures are justified)
|
| PAUSE! |
Ponder Plausability. |
Have you answered the question that was asked?
Yes, we have calculated the molar enthalpy of neutralisation in kJ mol-1
Is your solution to the question reasonable?
Acetic acid is a weak acid, so the heat released per mole of water formed will be less than that for a strong acid.
49 kJ mol-1 is less than 55.2 kJ mol -1, so our value is plausible.
Neutralisation reactions release heat, they are exothermic reactions, so the sign of the molar enthalpy of neutralisation is negative.
Our value, ΔneutH = −49 kJ mol -1 is negative so it is plausible.
|
| STOP! |
State the solution. |
What is the molar enthalpy of neutralisation?
ΔneutH = −49 kJ mol-1
|
↪ Back to top
Sample Question: Molar Enthalpy of Neutralisation
25.00 mL of 0.255 mol L-1 HCl(aq) is neutralised by exactly 19.73 mL of NaOH(aq). If the initial temperature of the reactants was 18.78 °C, calculate the final temperature of the mixture.
↪ Back to top
Footnotes:
(1) The Brønsted-Lowry equivalent proton-transfer reaction is :
H3O+(aq) + OH-(aq) → 2H2O(l)
This reaction will NOT be used in the following discussion because it produces 2 moles of water per mole of hydroxide ion used.
(2) see IUPAC Green Book, "Quantities, Units and Symbols in Physical Chemistry" Third Edition 2007
(3) A better method for measuring heat of neutralization is to use an adiabatic calorimeter fitted with an electrical heater.
A desciption of this type of calorimeter can be found in the calorimetry tutorial.
(4) You will find slightly different values quoted for molar heat of neutralisation mostly because the neutralisation reaction is dependent on the temperature at which the reaction occurs. In general the values you see quoted will be between 55 kJ mol-1 and 58 kJ mol-1 and refer to reactions that take place at ambient temperatures in a laboratory.
(5) The temperature is likely to decrease as more acid is added because the heat that was generated by the completed reaction is being dissipated in a greater mass of solution.
↪ Back to top

