Mass Spectroscopy and Isotopes Chemistry Tutorial

Key Concepts

• Elements occur as a mixture of isotopes.
• Different isotopes of an element have:

  (i) same number of protons
  so the atoms of the different isotopes have the same charge on the nucleus

  (ii) different number of neutrons
  so the mass of the atoms of one isotope is different to the mass of the atoms of a different isotope

• Mass Spectrometers use this difference in mass to separate the isotopes of an element from each other.
• A mass spectrum is the record of the amount of each isotope detected.
• Peak heights on a mass spectrum are proportional to the amount of each isotope present.
• Mass Spectroscopy data can then be used to determine the relative atomic mass of an element¹.

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Mass Spectrometer : General Principles

Step 1 sample is vaporised before entering mass spectrometer. M(s) → M(g) or M(l) → M(g) Step 2 Sample enters the low pressure ionisation chamber where an electron beam ionises the sample. M(g) → M+(g) + e- Step 3 Ions are accelerated to high speeds by an electric field. Step 4 Ions pass through a perpendicular magnetic field which bends the path of the ions dependent on their mass-to-charge ratio. Heavier ions are deflected less than lighter ions. Step 5 Ions with a particular mass reach the collector. Different masses can be collected by changing the magnetic or electric field. Step 6 The detector identifies the mass of each ion from its path. Data is recorded as a mass spectrum.

Example: Mass Spectrometer to Separate Isotopes

A sample of neon gas made up of 3 isotopes, 20Ne, 21Ne and 22Ne, is injected into the mass spectrometer. The sample passes through the electron beam which ionises the atoms of each isotope: 20Ne → 20Ne+ + e- (or   20Ne + e- → 20Ne+ + 2e-) 21Ne → 21Ne+ + e- (or   21Ne + e- → 21Ne+ + 2e-) 22Ne → 22Ne+ + e- (or   22Ne + e- → 22Ne+ + 2e-) The ions are accelerated and pass through slits in negatively charged metal plates (the second plate is more highly charged than the first). The ions enter the magnetic field where the path of the ions is deflected. Ions with the greatest mass (heavy isotopes) are deflected the least. The path of 20Ne+ is deflected more than 21Ne+ which is deflected more than 22Ne+ The voltage of the slits in the negatively charged plates is slowly raised causing the neon ion beams to sweep across the detector one by one. The ion detector is connected to a recorder which records the mass spectrum of the sample of neon gas. The mass spectrum shows the three isotopes of neon as three separate peaks. The height of each peak is related to the relative abundance of each isotope of neon. 20Ne+ has the highest peak so 20Ne is the most abundant isotope. 21Ne+ has the lowest peak so 21Ne is the least abundant isotope.

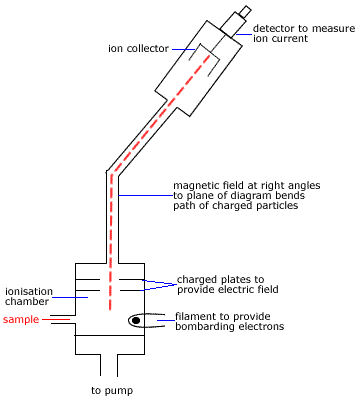
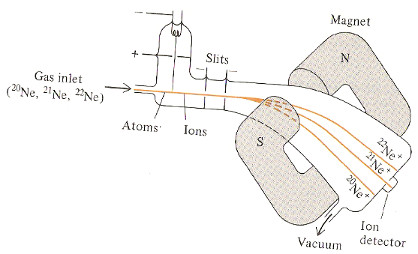
Example: Using a Mass Spectrum to Determine an Approximate Relative Atomic Mass of an Element

The mass spectrum could be presented in two ways, either giving the actual signal intensity for each isotope, or, giving you the relative peak heights or percentage abundances.

Signal Intensity Mass Spectrum of Neon	% Abundance Mass Spectrum of Neon
	% abundance mass number

Relative atomic mass (r.a.m.) = [(%abundance isotope a × mass isotope a) + (%abundance isotope b × mass isotope b) +(%abundance isotope c × mass isotope c)] ÷ 100

Mass number (A) can be used to approximate the mass of an isotope.
(see Relative Atomic Mass tutorial for details)

For the isotopes of neon:
the mass of ²⁰Ne ≈ A(neon-20) ≈ 20
the mass of ²¹Ne ≈ A(neon-21) ≈ 21
the mass of ²²Ne ≈ A(neon-22) ≈ 22

So the calculation for relative atomic mass (or atomic weight), now looks like this:

Relative atomic mass (Neon) = [(%abundance neon-20 × A_(neon-20)) + (%abundance neon-21 × A_(neon-21)) +(%abundance neon-22 × A_(neon-22))] ÷ 100

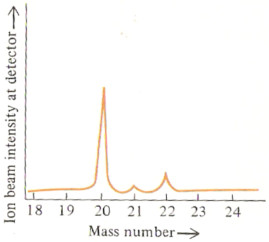
The % abundance of each isotope can be read directly off the second mass spectrum given above.

% abundance ²⁰Ne = 90.92 %
% abundance ²¹Ne = 0.26 %
% abundance ²²Ne = 8.82 %

Relative atomic mass (r.a.m.), or atomic weight, can then be calculated:

r.a.m. (Ne) = [(90.92 × 20) + (0.26 × 21) + (8.82 × 22)] ÷ 100
= [1818.4 + 5.46 + 194.04] ÷ 100
= 20.18

Example: Using a Mass Spectrum to Determine the Relative Atomic Mass of an Element

If the data you are provided with give you the actual mass² of each isotope (isotopic mass) as well as (or instead of) the mass number of each isotope, then you should use the actual isotopic masses in your calculation of relative atomic mass (r.a.m.).

Signal Intensity Mass Spectrum of Neon	Tabulated Data
	Mass Number Isotopic Mass % Abundance 20 19.992 90.92 21 20.994 0.26 22 21.991 8.82

Relative atomic mass (r.a.m.) = [(%abundance neon-20 × mass neon-20) + (%abundance neon-21 × mass neon-21) +(%abundance neon-22 × mass neon-22)] ÷ 100

r.a.m. (Ne) = [(90.92 × 19.992) + (0.26 × 20.994) + (8.82 × 21.991)] ÷ 100
= [1817.6 + 5.4584 + 193.96] ÷ 100
= 20.17

2. The mass of an isotope is not a whole number because the measured mass of a proton and of a neutron and of an electron is not a whole number. (Find out more at Mass Defect)