go to the AUS-e-TUTE homepage

Converting Concentration of Solution from One Unit to Another Chemistry Tutorial

Key Concepts

⚛ Concentration of a solution can be reported in units of mass of solute per unit volume of solution:

m/V,   %(m/V),   ppm,   c

⚛ We can convert one of these concentration units into another using the following relationships:

1 g = 1000 mg
1 g = 1 000 000 μg
(see Mass Units Conversion Tutorial)

1 L = 1000 mL
(see Volume Units Conversion Tutorial)

n = m ÷ M
(see Mass-mole Tutorial)

⚛ These concentration unit conversions are summarised in the table below: (1)

Concentration Units Conversion Table
 
Convert 		to m/V to %(m/V)
g/100 mL 		to ppm
μg mL-1 or mg L-1 		to c
mol L-1
g mL-1 g L-1
m/V
g mL-1 		  m×103 m×102 m×106 103 × m÷Mr
m/V
g L-1 		m÷103   m÷10 m×103 m÷Mr
%(m/V)
g/100 mL 		m÷102 m×10   m×104 10 × m÷Mr
ppm
μg mL-1 or mg L-1 		m ÷ 106 m ÷ 103 m ÷ 104   (m ÷ 103)/Mr
c
mol L-1 		c × Mr/103 c × Mr c × Mr/10 c × Mr × 103  

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

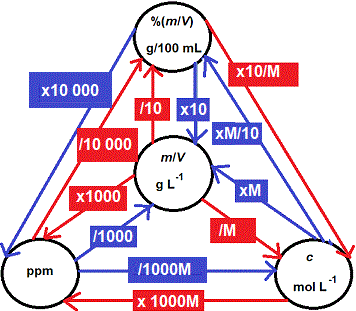
How to Convert Between Concentration Units

We can report the concentration of a solution in a number of different ways based on the volume of the solution:

⚛ mass concentration

symbol: m/V or w/v

units: g mL-1 or g L-1

⚛ mass-volume percentage concentration

symbol: %(m/V) or %(w/V)

units: g/100 mL or %

⚛ parts per million

symbol: ppm

units: mg L-1 or μg mL-1

⚛ amount of substance concentration (molarity)

symbol: c

units: mol L-1 (or M)

Note how the amount of substance concentration (molarity) is calculated:

c = moles of solute
volume of solution 		= n
V
c = mass of solute/molar mass of solute
volume of solution 		= m/M
V

Can you see that ALL of the concentration units above are based on:

Therefore we can use the mass concentration (m/V or w/V) as the basis for converting between all these different units.(2)

If, for example, we make an aqueous solution of copper(II) sulfate, CuSO(aq), by dissolving 0.250 g of solid copper(II) sulfate, CuSO4(s), in enough water to make 250.0 mL of solution, then the mass concentration of the solution can be calculated:

mass concentration = m/V = 0.250 g ÷ 250.0 mL = 0.00100 g mL-1

and because there are 1000 mL in 1 L, we could also determine mass concentration in units of grams of solute per litre of solution:

mass concentration = 0.00100 g mL-1 × 1000 mL/L = 1.00 g L-1

In general:
1000 × (m/V g mL-1) = m/V g L-1

Mass-volume percentage concentration, %(m/V), has the units grams of solute per 100 mL of solution. So we can convert mass concentration in g mL-1 to g/100 mL by multiplying the mass and the volume in the mass concentration by 100:

%(m/V) = m (g) × 100
V (mL) × 100

For our copper(II) sulfate solution with a mass concentration of 0.00100 g mL-1, we can calculate the concentration as a mass-volume percentage concentration as shown below:

%(m/V) = m (g) × 100
V (mL) × 100 		= 0.00100 (g) × 100
1 (mL) × 100 		= 0.100 g
100 mL

Note that the mass-volume percentage concentration may be given as 0.100 g/100 mL or as 0.100 %(m/V)

In general:
100 × (m/V g mL-1) = %(m/V) or g/100 mL

The units for parts per million concentration (ppm) are μg mL-1.
There are 1 million micrograms in a gram, 1 000 000 μg = 1 g
So we can convert mass concentration in g mL-1 to μg mL-1 by multiplying the mass ONLY by 1 000 000 :

ppm = m (g) × 1 000 000 μg/g
V (mL)

For our copper(II) sulfate solution with a mass concentration of 0.00100 g mL-1, we can calculate the concentration as a μg L-1 as shown below:

ppm = m (g) × 1 000 000 μg/g
V (mL) 		= 0.00100 g × 1 000 000 μg/g
1 mL 		= 1000 μg
1 mL

The concentration could be recorded as 1000 μg mL-1 or as 1000 ppm.

Because there are 1000 mL in 1 L and 1000 μg in 1 mg, we could convert this parts per million concentration in μg of solute per mL of solution to a parts per million concentration in mg of solute per litre of solution by dividing the mass in μg by 1000 and dividing the volume in mL by 1000.
So we can convert the concentration of our copper(II) sulfate solution from μg mL-1 to mg L-1 as shown below:

ppm = = 1000 μg ÷ 1000 μg/mg
1 mL ÷ 1000 mL/L 		= 1 mg
0.001 L 		= 1000 mg
1 L

The concentration of our copper(II) sulfate solution could therefore be reported as 1000 mg L-1 or 1000 ppm

In general:
1 000 000 × (m/V g mL-1) = ppm (either μg mL-1 or mg L-1)

The units for amount of substance concentration, molarity, are moles of solute per litre of solution.
Moles of solute is calculated by dividing the mass of the solute in grams by the molar mass of the solute in grams per mol:

n(solute) mol = m(solute) g ÷ M(solute) g mol-1

We can use the periodic table to find the atomic weight (atomic mass) of each element and use this to calculate the molar mass of the solute (relative molecular mass expressed in grams).
For CuSO4:

M(CuSO4) = Mr(Cu) + Mr(S) + 4×Mr(O)

M(CuSO4) = 63.55 + 32.06 + 4×16.00 = 159.61 g mol-1

Mass concentration can be expressed in units of g L-1.
Our copper(II) sulfate solution has a mass concentration of 1 g L-1.
We can convert this to mol L-1 by dividing the mass of solute by its molar mass :

c mol L-1 = = m g/Mr g mol-1
V L 		= 1 g/159.61 g mol-1
1 L 		= 0.00627 mol L-1

In general:
1 000 × [(m ÷ Mr)/V] g mL-1 = c mol L-1
[(m ÷ Mr)/V] g L-1 = c mol L-1

It is worth noting the special relationship between %(m/V) and ppm :

%(m/V) gives us the concentration in parts of solute per 100 parts of solution (that is, a percentage)

ppm gives us the concentration in parts of solute per 1 000 000 parts of solution (that is, parts per million)

Therefore, to convert %(m/V) to ppm, we multiply it by a factor of 1 000 000/100 = 10 000

The %(m/V) of our CuSO4(aq) is 0.1 g/100 mL (or 0.001 %) so its concentration in ppm is:

ppm = 10 000 × %(m/V) = 10 000 × 0.1 g/100 mL = 1000 ppm

In general:
10 000 × %(m/V) = ppm (either mg L-1 or μg mL-1)

It is also worth noting that a mass concentration (m/V) given in units of g L-1 could also be expressed as g/1000 mL, or parts per thousand.
So to convert a parts per thousand concentration, g L-1, to parts per hundred, %(m/V), we only need to divide by 10: (m/V) ÷ 10 = %(m/V)
To convert a parts per thousand concentration, g L-1 or g/1000 mL, to parts per million, we just multiply by 1000: (m/V) × 1000 = ppm (either μg mL-1 or mg L-1)

You should practise converting one concentration unit to another, for example, how would you convert parts per million (ppm) to an amount of substance concentration (molarity) ?
You can check your calculations using the summary table in the next section.

↪ Back to top

Summary Table: Converting Concentration Units

The general relationships between the various concentration units are summarised in the table below:

Concentration Units Conversion Table
 
Convert 		to m/V to %(m/V)
g/100 mL 		to ppm
μg mL-1 or mg L-1 		to c
mol L-1
g mL-1 g L-1
m/V
g mL-1 		  m×103 m×102 m×106 103 × m÷Mr
m/V
g L-1 		m÷103   m÷10 m×103 m÷Mr
%(m/V)
g/100 mL 		m÷102 m×10   m×104 10 × m÷Mr
ppm
μg mL-1 or mg L-1 		m ÷ 106 m ÷ 103 m ÷ 104   (m ÷ 103)/Mr
c
mol L-1 		c × Mr/103 c × Mr c × Mr/10 c × Mr × 103  

Let's say we have a 0.150 mol L-1 aqueous solution of sodium chloride, NaCl(aq).
Mr(NaCl) = 22.99 + 35.45 = 58.44 g mol-1
We can use the conversion table above to convert molarity (mol L-1) to a concentration in g mL-1, g L-1, %(m/V), and ppm.

Concentration Units Conversion Table for 0.150 mol L-1 NaCl(aq)
 
Convert 		to m/V to %(m/V)
g/100 mL 		to ppm
μg mL-1 or mg L-1		 to c
g mL-1 g L-1
c
mol L-1 		c × Mr/103 c × Mr c × Mr/10 c × Mr × 103  
c(NaCl(aq))
= 0.150 mol L-1 		0.150 × 58.44/103
= 0.00877 g mL-1 		0.150 × 58.44
= 8.77 g L-1 		0.150 × 58.44/10
= 0.877 g/100 mL		 0.150 × 58.44 × 103
= 8766 ppm 		 

The saline solution, NaCl(aq), used in medicine to clean wounds or store contact lenses, has a concentration of 0.90 (m/V)%, we convert this to other units of concentration using the summary table as shown below:

Concentration Units Conversion Table for 0.90 %(m/V) NaCl(aq)
 
Convert 		to m/V to %(m/V) to ppm
μg mL-1 or mg L-1		 to c
mol L-1
g mL-1 g L-1
%(m/V)
g/100 mL 		m÷102 m×10   m×104 10 × m÷Mr
0.90%(m/V)
0.90 g/100 mL-1 		0.90÷102 = 0.0090 g mL-1 0.90×10 = 9.0 g L-1   0.90×104 = 9 000 ppm 10 × 0.90÷58.44 = 0.15 mol L-1

↪ Back to top

Summary Diagram: Converting Concentration Units

The information in the table above can be used to construct a diagram:

converting concentration units

To use this diagram:

  1. Choose a concentration unit to begin
  2. follow the arrow (red or blue) to the concentration unit you need
  3. follow the instruction given in the red or blue box

For example, in Australia, an adult cannot legally drive a car with a blood alcohol level above 0.05% (0.05 g of alcohol per 100 mL of blood).
Convert this to a blood alcohol concentration in parts per million.

  1. Locate %(m/V) (g/100 mL) on the diagram (top circle)
  2. Follow the blue line to ppm
  3. Follow the instruction given: %(m/V) × 10 000 = 0.05 × 10 000 = 500 ppm

For example, if the amount of substance concentration (molarity) of NaOH(aq) is 0.250 mol L-1, what is its concentration in ppm?
M(NaOH) = 22.99 + 16.00 + 1.008 = 39.998 mol L-1

  1. Locate molarity (c) on the diagram (bottom right circle)
  2. Follow the red line to ppm
  3. Follow the instruction given: c × 1000M = 0.250 × 1000 × 39.998 = 9999.5 ppm

↪ Back to top

Worked Examples: Converting Concentration Units

Question 1: The mass concentration of citric acid in a sample of orange juice was 45 g L-1.
What is the concentration of citric acid in this orange juice in parts per million ?

Solution:

Step 1: Extract the data from the question:

m/V(citric acid) = 45 g L-1
ppm = ?

Step 2: What is the relationship between what you know and what you need to find out?

1 ppm = 1 mg L-1
1000 mg = 1 g
m/V(g L-1) × 1000 mg/g = 1000 × m/V = ppm (mg L-1)

Step 3: Perform the calculations:

m/V(45 g L-1) × 1000 mg/g = 45 000 mg L-1
1 ppm = 1 mg L-1
45 000 mg L-1 = 45 000 ppm

Question 2: The concentration of oxygen gas dissolved in a water sample is 6.5 ppm.
What is the mass-volume percentage concentration of oxygen gas in this water sample ?

Solution:

Step 1: Extract the data from the question:

concentration(oxygen gas) = 6.5 ppm
%(m/V) = ? g/100 mL

Step 2: What is the relationship between what you know and what you need to find out?

1 ppm = 1 μg mL-1
1 μg mL-1 ÷ 1 000 000 μg/g = 1 g mL-1
(100 × 1) g ÷ (100 × 1 mL) = %(mV) g/100 mL

Step 3: Perform the calculations:

6.5 ppm = 6.5 μg mL-1
6.5 μg mL-1 ÷ 1 000 000 μg/g = 6.5×10-6 g mL-1
%(mV) = (100 × 6.5×10-6) g ÷ (100 × 1 mL) = 6.5×10-4 g/100 mL = 0.00065 %(m/V)

Question 3: Atheltes often consume a "sports drink", an aqueous solution of electrolytes like chloride ions, to replace ions that they lost in sweat.
One sample of "sports drink" had a chloride ion concentration of 675 ppm.
Calculate the amount concentration (molarity) of chloride ions in this "sports drink".

Solution:

Step 1: Extract the data from the question:

concentration(Cl-(aq)) = 675 ppm
c(Cl-(aq)) = ? mol L-1

Step 2: What is the relationship between what you know and what you need to find out?

1 ppm = 1 mg L-1
1 g = 1000 mg
n(Cl-(aq)) = (m(Cl-(aq) in mg/1000 mg/g) ÷ M(Cl-(aq)) = ? mol
c(Cl-(aq)) = n(Cl-(aq)) ÷ V

Step 3: Perform the calculations:

675 ppm = 675 mg L-1
n(Cl-(aq)) = (675 mg/1000 mg/g) ÷ 35.45 g mol-1 = 0.0190 mol
c(Cl-(aq)) = 0.0190 mol ÷ 1 L = 0.0190 mol L-1

↪ Back to top

Problem Solving: Converting One Concentration Unit Into Another

Below is a worked example of how to convert the concentration given in one unit to a concentration in different units.

The Problem: The active ingredient in bleach is sodium hypochlorite, NaOCl(aq).(3) The bleach you buy from the supermarket has a sodium hypochlorite concentration of 5.25 %(m/V).

Determine the amount of substance concentration (molarity) of sodium hypochlorite in bleach.

Solving the Problem using the StoPGoPS model for problem solving:

STOP!
 State the question. What is the question asking you to do?

Determine (calculate) the amount of substance concentration (molarity)

c(NaOCl(aq)) = ? mol L-1

PAUSE!
 Pause to Plan. What information (data) have you been given?

  • molecular formula for sodium hypochlorite: NaOCl
  • %(m/V) = 5.25 % = 5.25 g/100 mL

What is your plan for solving this problem?

Step 1: Calculate the molar mass of NaOCl using the periodic table: M(NaOCl) = ? g mol-1

M(NaOCl) = M(Na) + M(O) + M(Cl)

Step 2: Calculate the moles of NaOCl in 100 mL of bleach

n(NaOCl) = m(NaOCl) ÷ M(NaOCl)

Step 3: Calculate the moles of NaOCl in 1 L of bleach (molarity)

c(NaOCl) = n(NaOCl) ÷ [V(NaOCl) 100 mL/1000 mL L-1]

GO!
 Go with the Plan.

Step 1: Calculate the molar mass of NaOCl using the periodic table: M(NaOCl) = ? g mol-1

M(NaOCl) = M(Na) + M(O) + M(Cl)

M(NaOCl) = 22.99 + 16.00 + 35.45 = 74.44

Step 2: Calculate the moles of NaOCl in 100 mL of bleach

n(NaOCl) = m(NaOCl) ÷ M(NaOCl)

n(NaOCl) = 5.25 ÷ 74.44 = 0.07053 mol/100 mL

Step 3: Calculate the moles of NaOCl in 1 L of bleach (molarity)

c(NaOCl) = n(NaOCl) ÷ [V(NaOCl) 100 mL/1000 mL L-1]

c(NaOCl) = 0.07053 ÷ 100 mL/1000 mL L-1] = 0.705 mol L-1

(Note: only 3 significant figures are justified)

PAUSE!
 Ponder Plausability. Have you answered the question that was asked?

Yes, we have calculated the molarity.

Is your solution to the question reasonable?

Use the summary table or diagram above to check the answer:
c = %(m/V) × (10/M) = 5.25 × (10/74.44) = 0.705 mol L-1
Since this is the same as the molarity calculated above, we are reasonably confident that our value is plausible.
STOP!
 State the solution. What is the amount of substance concentration (molarity)?

c(NaOCl(aq)) = 0.705 mol L-1

↪ Back to top

Sample Question

The concentration of chloride ions in sample of river water is 4.2 ppm.

Calculate the mass concentration of chloride ions in g L-1.

m/V(Cl-(aq)) = g L-1

↪ Back to top

Footnotes:

(1) Symbols used in this tutorial are those recommended by IUPAC, see "Green Book", Quantities, Units and Symbols in Physical Chemistry Third Edition

(2) Note that the volume of solution is dependent on temperature (and to a lesser extent on lab pressure), hence it is assumed that you are converting between concentration units for solutions at constant temperature and pressure.

(3) You may also fnd the molecular formula of sodium hypochlorite given as NaOCl. IUPAC recommends NaClO instead of NaOCl. Refer to IUPAC Red Book Nomenclature of Inorganic Chemistry 2005

↪ Back to top