go to the AUS-e-TUTE homepage

Acid-Base Titration Curves Tutorial

Key Concepts

  1. The equivalence point1 of an acid-base reaction.
    (amount of acid and of base is just sufficient to cause complete consumption of both the acid and the base.)

  2. The pH of the solution at the equivalence point.
    (which is dependent on the strength of the acid and strength of the base used in the titration)

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Analysing a Titration Curve

Determining whether acid has been added to base, or base has been added to acid.

Consider the titration curve shown below for a particular acid-base reaction:

pH of solution
in conical (erlenmeyer) flask		 A Titration Curve

volume of reactant added
from burette (buret) (mL)
  • Before the experiment begins, no reactant has been added from the burette (buret).
    Volume of reactant added from the burette (buret) is 0.00 mL.

  • From the graph, the pH of the solution in the conical (erlenmeyer) flask before the experiment has begun is 13.00
    (move your cursor to a point on the graph to see its coordinates)

  • By the end of the experiment, 14.00 mL of reactant from the burette (buret) have been added, and the pH of the solution in the conical (erlenmeyer) flask has dropped to 1.78

  • Overall, the pH of the solution in the conical (erlenmeyer) flask has decreased from 13.00 to 1.78

  • A decrease in pH means that the solution has become more acidic.

  • In this titration an acid has been added to a base.

  • At the beginning of the experiment, the conical (erlenmeyer) flask contained a base with a pH of 13.00 and the burette (buret) contained an acid.

Determining the equivalence point for the acid-base reaction

Consider the same titration curve as discussed above:

pH of solution
in conical (erlenmeyer) flask		 A Titration Curve

volume of acid added
from burette (buret) (mL)		 There are 3 distinct regions to the titration curve:
  1. Initially, addition of the acid from the burette (buret) does not change the pH of the solution in the conical (erlenmeyer) flask by very much.
    The base is the reactant in excess in the conical (erlenmeyer) flask:
    moles of OH- > moles of H+

    All the acid added from the burette (buret) is being consumed in the reaction, the acid is the limiting reagent:
    H+ + OH- → H2O

  2. Dramatic pH change: The addition of a small amount of acid from the burette (buret) causes the pH of the solution to change dramatically.
    The equivalence point for this acid-base reaction lies within this range.
    at the equivalence point: moles OH- = moles H+

  3. Finally, addition of acid does not change the pH of the solution in the conical (erlenmeyer) flask by very much.
    All the base has already been consumed in reaction with acid, the base is now the limiting reagent.
    The acid is now the reactant in excess in the conical (erlenmeyer) flask.
    moles H+ > moles OH-

    The pH of the solution in the conical (erlenmeyer) flask is dependent on the slight changes in concentration of acid in the flask.

The equivalence point is estimated to be at the mid-point of the "vertical section" of the titration curve2:

pH of solution
in conical (erlenmeyer) flask		 A Titration Curve

volume of acid added
from burette (buret) (mL)		 The mid-point of the vertical section of the graph lies half way between the points:

  • (9.90,10.70) that is, the point at which 9.90 mL of acid have been added and the pH of the solution is 10.70

  • and (10.10,3.3) that is, the point at which 10.10 mL of acid have been added and the pH of the solution is 3.3

At the equivalence point, the volume of acid that has been added to the base will be half way between 9.90 mL and 10.10 mL
volume of acid added at equivalence point = (9.90 + 10.10) ÷ 2 = 10.00 mL
When the titration curve shows a section that is almost exactly vertical, we can read the volume of acid added at the equivalence point directly off the graph by extending the "vertical section" of the graph to meet the horizontal axis as shown in green.

We can see that at the equivalence point, 10.0 mL of acid from the burette (buret) has been added to the base in the conical (erlenmeyer) flask.

Determining the pH of the solution at the equivalence point

pH of solution
in conical (erlenmeyer) flask		 A Titration Curve

volume of acid added
from burette (buret) (mL)		 The pH at the equivalence point of the titration is at the mid-point of the vertical section of the graph so it lies half way between the points:

  • (9.90,10.70) that is, the point at which 9.90 mL of acid have been added and the pH of the solution is 10.70

  • and (10.10,3.3) that is, the point at which 10.10 mL of acid have been added and the pH of the solution is 3.3

The pH at the equivalence point will be half way between pH = 10.70 and pH = 3.3
pH at equivalence point = (10.70 + 3.30) ÷ 2 = 7.0

At the equivalence point:

  • 10.0 mL of acid have been added from the burette (buret) to the conical (erlenmeyer) flask

  • the pH of the solution in the conical (erlenmeyer) flask is now 7

The pH of the solution at the equivalence point of an acid-base reaction at 25oC tells us about the relative strengths of the acid and base used in the titration experiment:

Do you know this?

Join AUS-e-TUTE!

Play the game now!

Examples of Titration Curves (aqueous solutions at 25o)

The table below shows the general features of titration curves produced as a result of using aqueous solutions of different strengths of monoprotic acids and monobases in titration experiments conducted at 25°C.3

General Type Example Typical Titration Curve Features of Curve
Strong Acid
added to
Strong Base		 HCl(aq) added to NaOH(aq)

Calculate a Titration Curve

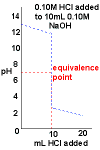  • Curve begins at high pH, a basic pH

  • Curve ends ends at low pH, an acidic pH.

  • Rapid change in pH near the equivalence point.

  • pH = 7 at the equivalence point.
Strong Base
added to
Strong Acid		 NaOH(aq) added to HCl(aq)

Calculate a Titration Curve

  • Curve begins at low pH, an acidic pH

  • Curve ends ends at high pH, a basic pH.

  • Rapid change in pH near the equivalence point.

  • pH = 7 at the equivalence point.
Strong Base
added to
Weak Acid		 NaOH(aq) added to acetic acid, CH3COOH(aq)
(See determination of acetic acid in vinegar)
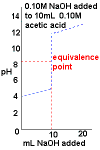  • Curve begins at low pH, an acidic pH

  • Curve ends ends at high pH, a basic pH.

  • Rapid change in pH near the equivalence point.

  • pH > 7 at the equivalence point.
Weak Base
added to
Strong Acid		 Ammonia, NH3(aq), added to HCl(aq)
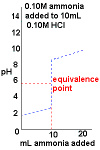  • Curve begins at low pH, an acidic pH

  • Curve ends ends at high pH, a basic pH.

  • Rapid change in pH near the equivalence point.

  • pH < 7 at the equivalence point.
Weak Base
added to
Weak Acid		 Ammonia, NH3(aq), added to acetic acid, CH3COOH(aq)
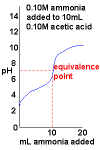  • Curve begins at low pH, an acidic pH

  • Curve ends ends at high pH, a basic pH.

  • No dramatic change in pH near the equivalence point.
    This means this is a very difficult titration to perform.

  • pH at the equivalence point will depend on the relative strengths of the acid and base used.

Do you understand this?

Join AUS-e-TUTE!

Take the test now!

1. 1 equivalent of an acid is the quantity of that acid which will donate 1 mole of H+.
1 equivalent of a base is the quantity which supplies 1 mole of OH-.
At the equivalence point, 1 equivalent of acid neutralises 1 equivalent of base.

2. The pH at the equivalence point can be calculated: pH = ½pKa + ½pKw + ½log10(mMAo/mφ)
Ka is the acid dissociation constant for the acid and pKa = -log10Ka
Kw is the dissociation constant for water and pKw = -log10Kw
mMAo refers to the molality of the salt formed and mφ to a standard molality of 1 mol/kg,
For a strong acid being titrated with a strong base, the acid is completely dissociated, Ka is infinite, so pKa is effectively 0, and at the equivalence point all the acid has been converted to salt and water, and the salt is completely dissociated so that mMAo/mφ = 0,
then for a strong acid - strong base titration at the equivalence point at 25oC: pH = ½pKw = ½(-log10Kw) = ½(-log1010-14) = 7

3. An example of a titration curve for a strong diprotic acid - strong monobase can be found here

Note that the pH of the solution at the equivalence point is also dependent on temperature, unless otherwise specified a temperature of 25°C is assumed. See Ion Product for Water, Kw